Implement Queue using Stacks

-

Implement Queue using Stacks

A Queue is defined by its property of FIFO, which means First in First Out, i.e the element which is added first is taken out first. This behaviour defines a queue, whereas data is actually stored in an array or a list in the background.
What we mean here is that no matter how and where the data is getting stored, if the first element added is the first element being removed and we have implementation of the functions enqueue()and dequeue() to enable this behaviour, we can say that we have implemented a Queue data structure.
In our previous tutorial, we used a simple array to store the data elements, but in this tutorial we will be using Stack data structure for storing the data.
While implementing a queue data structure using stacks, we will have to consider the natural behaviour of stack too, which is First in Last Out.
For performing enqueue we require only one stack as we can directly push data onto the stack, but to perform dequeue we will require two Stacks, because we need to follow queue's FIFO property and if we directly pop any data element out of Stack, it will follow LIFO approach(Last in First Out).

Implementation of Queue using Stacks

In all we will require two Stacks to implement a queue, we will call them S1 and S2.
class Queue {
    public:
    Stack S1, S2;
    
    //declaring enqueue method
    void enqueue(int x);
    
    //declaring dequeue method
    int dequeue();
}

In the code above, we have simply defined a class Queue, with two variables S1 and S2 of type Stack.
We know that, Stack is a data structure, in which data can be added using push() method and data can be removed using pop() method.
You can find the code for Stack class in the Stack data structure tutorial.
To implement a queue, we can follow two approaches:
  1. By making the enqueue operation costly
  2. By making the dequeue operation costly

1. Making the Enqueue operation costly

In this approach, we make sure that the oldest element added to the queue stays at the top of the stack, the second oldest below it and so on.
To achieve this, we will need two stacks. Following steps will be involved while enqueuing a new element to the queue.
NOTE: First stack(S1) is the main stack being used to store the data, while the second stack(S2) is to assist and store data temporarily during various operations.
  1. If the queue is empty(means S1 is empty), directly push the first element onto the stack S1.
  2. If the queue is not empty, move all the elements present in the first stack(S1) to the second stack(S2), one by one. Then add the new element to the first stack, then move back all the elements from the second stack back to the first stack.
  3. Doing so will always maintain the right order of the elements in the stack, with the 1st data element staying always at the top, with 2nd data element right below it and the new data element will be added to the bottom.
This makes removing an element from the queue very simple, all we have to do is call the pop()method for stack S1.

2. Making the Dequeue operation costly

In this approach, we insert a new element onto the stack S1 simply by calling the push() function, but doing so will will push our first element towards the bottom of the stack, as we insert more elements to the stack.
But we want the first element to be removed first. Hence in the dequeue operation, we will have to use the second stack S2.
We will have to follow the following steps for dequeue operation:
  1. If the queue is empty(means S1 is empty), then we return an error message saying, the queue is empty.
  2. If the queue is not empty, move all the elements present in the first stack(S1) to the second stack(S2), one by one. Then remove the element at the top from the second stack, and then move back all the elements from the second stack to the first stack.
  3. The purpose of moving all the elements present in the first stack to the second stack is to reverse the order of the elements, because of which the first element inserted into the queue, is positioned at the top of the second stack, and all we have to do is call the pop() function on the second stack to remove the element.
NOTE: We will be implementing the second approach, where we will make the dequeue()method costly.

Adding Data to Queue - enqueue()

As our Queue has a Stack for data storage instead of arrays, hence we will be adding data to Stack, which can be done using the push() method, therefore enqueue() method will look like:
void Queue :: enqueue(int x) 
{
    S1.push(x);
}
That's it, new data element is enqueued and stored in our queue.

Removing Data from Queue - dequeue()

When we say remove data from Queue, it always means taking out the element which was inserted first into the queue, then second and so on, as we have to follow the FIFO approach.
But if we simply perform S1.pop() in our dequeue method, then it will remove the Last element inserted into the queue first. So what to do now?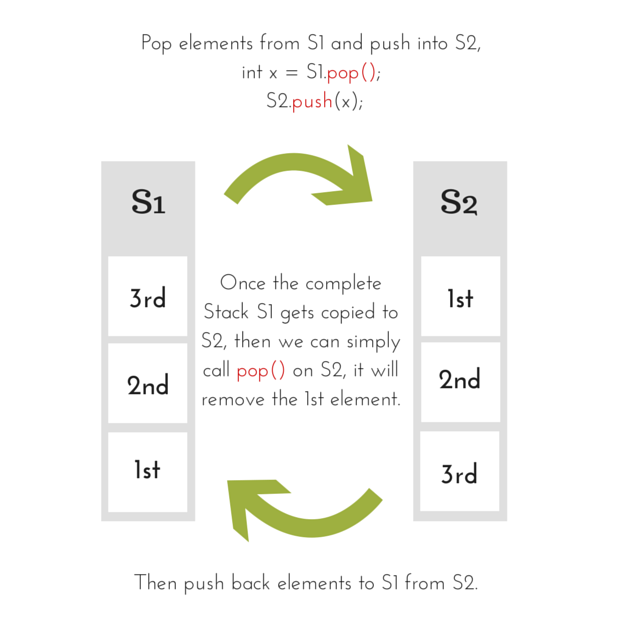
Implementing Queue using Stack
As you can see in the diagram above, we will move all the elements present in the first stack to the second stack, and then remove the top element, after that we will move back the elements to the first stack.
int Queue :: dequeue() 
{
    int x, y;
    while(S1.isEmpty()) 
    {
        // take an element out of first stack
        x = S1.pop();
        // insert it into the second stack
        S2.push();
    }
  
    // removing the element
    y = S2.pop();
  
    // moving back the elements to the first stack
    while(!S2.isEmpty()) 
    {
        x = S2.pop();
        S1.push(x);
    }
  
    return y;
}
Now that we know the implementation of enqueue() and dequeue() operations, let's write a complete program to implement a queue using stacks.

Implementation in C++(OOPS)

We will not follow the traditional approach of using pointers, instead we will define proper classes, just like we did in the Stack tutorial.
/*  Below program is written in C++ language  */

# include<iostream>

using namespace std;

// implementing the stack class
class Stack
{
    int top;
    public:
    int a[10];  //Maximum size of Stack
    Stack()
    {
        top = -1;
    }
    
    // declaring all the function
    void push(int x);
    int pop();
    bool isEmpty();
};

// function to insert data into stack
void Stack::push(int x)
{
    if(top >= 10)
    {
        cout << "Stack Overflow \n";
    }
    else
    {
        a[++top] = x;
        cout << "Element Inserted into Stack\n";
    }
}

// function to remove data from the top of the stack
int Stack::pop()
{
    if(top < 0)
    {
        cout << "Stack Underflow \n";
        return 0;
    }
    else
    {
        int d = a[top--];
        return d;
    }
}

// function to check if stack is empty
bool Stack::isEmpty()
{
    if(top < 0)
    {
        return true;
    }
    else
    {
        return false;
    }
}

// implementing the queue class
class Queue {
    public:
    Stack S1, S2;
    
    //declaring enqueue method
    void enqueue(int x);
    
    //declaring dequeue method
    int dequeue();
};

// enqueue function
void Queue :: enqueue(int x) 
{
    S1.push(x);
    cout << "Element Inserted into Queue\n";
}

// dequeue function
int Queue :: dequeue() 
{
    int x, y;
    while(!S1.isEmpty()) 
    {
        // take an element out of first stack
        x = S1.pop();
        // insert it into the second stack
        S2.push(x);
    }
  
    // removing the element
    y = S2.pop();
  
    // moving back the elements to the first stack
    while(!S2.isEmpty()) 
    {
        x = S2.pop();
        S1.push(x);
    }
  
    return y;
}

// main function
int main()
{
    Queue q;
    q.enqueue(10);
    q.enqueue(100);
    q.enqueue(1000);
    cout << "Removing element from queue" << q.dequeue();
    
    return 0;
}

Comments

Post a Comment

Thanks for comment. We will get back to you soon...

Popular posts from this blog

Difference between Array and Linked List

-
Image
Linked List vs. Array Array is a datatype which is widely implemented as a default type, in almost all the modern programming languages, and is used to store data of similar type. But there are many usecases, like the one where we don't know the quantity of data to be stored, for which advanced data structures are required, and one such data structure is  linked list . Let's understand how array is different from Linked list. ARRAY LINKED LIST Array is a collection of elements of similar data type. Linked List is an ordered collection of elements of same type, which are connected to each other using pointers. Array supports  Random Access , which means elements can be accessed directly using their index, like  arr[0]  for 1st element,  arr[6]  for 7th element etc. Hence, accessing elements in an array is  fast  with a constant time complexity of  O(1) . Linked List supports  Sequential Access , which means to access any element/node in a linked list, we have to
Read more

What is a Queue Data Structure?

-
Image
What is a Queue Data Structure? Queue  is also an abstract data type or a linear data structure, just like stack data structure, in which the first element is inserted from one end called the  REAR (also called  tail ), and the removal of existing element takes place from the other end called as  FRONT (also called  head ). This makes queue as  FIFO (First in First Out) data structure, which means that element inserted first will be removed first. Which is exactly how queue system works in real world. If you go to a ticket counter to buy movie tickets, and are first in the queue, then you will be the first one to get the tickets. Right? Same is the case with Queue data structure. Data inserted first, will leave the queue first. The process to add an element into queue is called  Enqueue  and the process of removal of an element from queue is called  Dequeue . Basic features of Queue Like stack, queue is also an ordered list of elements of similar data types. Queue is
Read more

Tree Traversal Techniques

-
Image
Traversal  is the method of processing each and every node in the Binary Search Tree exactly once in a systematic manner. There are three different types of tree traversal. (1) Preorder Traversal  (2) In order Traversal  (3) Post order Traversal PreOrder Traversal Steps for Preorder Traversal: (1) Process the root node first. (2) Traverse the left sub tree in preorder. (3) Traverse the right sub tree in preorder. InOrder Traversal Steps for Inorder Traversal: (1) Traverse the left sub tree in inorder. (2) Process the root node. (3) Traverse the right sub tree in inorder. PostOrder Traversal Steps for PostOrder Traversal: (1) Traverse the left sub tree in Post order. (2) Traverse the right sub tree in Post order. (3) Process the root node. Now Consider Following Example PreOrder Traversal :  A B D E C F G  InOrder Traversal :  D B E A F C G PostOrder Traversal :  D E B F G C A
Read more